Programmes de tri

Introduction

Dans cette partie, nous allons montrer comment créer des programmes de tri sur des tableaux. Ces programmes sont basés sur des algorithmes de tri classiques enseignés dans toutes les filières de formation à la programmation.

Tri par sélection

Le tri par sélection consiste à parcourir un tableau de valeurs pour sélectionner la plus grande valeur et la placer en première position. Ensuite, il suffit de parcourir à nouveau le tableau pour placer la deuxième plus grande valeur et ainsi de suite. 

Construction du tri par sélection

La vidéo présente comment construire un programme basé sur ce principe. Plusieurs méthodes sont possibles répondant à ce principe. Dans cette version, pour placer la plus grande valeur à l’indice i, on compare successivement les valeurs d’indice supérieur. Dès qu’une valeur est plus grande, on l’échange avec la valeur d’indice i.

Programme AlgoTouch de tri par sélection

Voici un programme similaire réalisé avec la version web d’AlgoTouch. Dans ce programme les données sont triées par ordre croissant. Pour commencer, la plus petite valeur est placée en première position, puis la plus petite valeur suivante est placée en seconde position, etc.  Contrairement à l’algorithme précédent, à une étape donnée i, l’algorithme utilisé cherche la position de la plus petite valeur (son indice) avant de la mettre à sa place par échange avec la position i. Dans la version précédente, à chaque fois qu’une valeur était plus petite que la valeur courante, on l’échangeait avec la valeur courante.

On peut lancer le programme triSelection soit en mode pas à pas, soit en mode automatique, soit en mode sans interruption. On peut aussi voir comment fonctionne le programme positionMin en le lançant après plusieurs étapes de triSelection. La encore, les modes pas à pas et automatique sont à privilégier.

Tri par insertion

Le tri par insertion repose sur le principe suivant: si les n premières valeurs du tableau sont déjà triées, placer la valeur suivante consiste à l’insérer parmi ces valeurs.

Construction du tri par insertion

Plusieurs programmes permettent de réaliser le tri par insertion. Cette vidéo présente une version dans laquelle lorsqu’il s’agit d’insérer l’élément d’indice i dans le sous tableau t[0..i-1], on l’échange avec l’élément d’indice i-1. Puis on recommence si nécessaire en échangeant avec l’élément d’indice i-2, jusqu’à ce qu’il soit correctement placé.

Programme AlgoTouch de tri par insertion

Voici une version du tri par insertion en AlgoTouch. Le principe général de l’algorithme reste le même: à l’étape k, la valeur a[k] est placée correctement dans le tableau. Les éléments d’indice inférieur à k sont décalés à droite par échange avec la valeur de a[k] tant qu’ils sont supérieurs.

On peut lancer le programme TriInsertion soit en mode pas à pas, soit en mode automatique, soit en mode sans interruption. On peut aussi voir comment fonctionne le programme InsereSuivant en le lançant après plusieurs étapes de TriInsertion. La encore, les modes pas à pas et automatique sont à privilégier.

Programme AlgoTouch de tri par insertion amélioré

Voici une autre version du tri par insertion en AlgoTouch. Le principe général de l’algorithme reste le même. Seule la méthode pour insérer une valeur est différente. Dans la version précédente, la valeur à insérer est déplacée progressivement vers sa place définitive par échange avec la valeur d’indice précédent. En fait, ceci entraîne des déplacements inutiles! Dans cette version, à l’étape k, la valeur a[k] est placée dans une variable val puis les éléments d’indice inférieur à k sont décalés à droite tant qu’ils sont supérieurs à val. Pour terminer, la valeur de val est copiée à sa place en une seule fois.
On peut lancer le programme TriInsertion soit en mode pas à pas, soit en mode automatique, soit en mode sans interruption. On peut aussi voir comment le programme InsererEltOrdreK fonctionne en le lançant après plusieurs étapes de TriInsertion. La encore, les modes pas à pas et automatique sont à privilégier.

Tri à bulles

Le principe du tri à bulles est très simple. Parcourir un tableau, tant que deux éléments consécutifs sont non ordonnés, les échanger. Parcourir le tableau de données à nouveau  et s’arrêter lorsqu’aucun échange n’a été effectué. Cela signifie que les éléments sont dans l’ordre.

Programme de tri à bulles

Voici un programme de tri bulles en AlgoTouch qui s’inspire du principe énoncé plus haut.
Une variable permut, initialisée à 0,  est utilisée pour savoir si une permutation à été effectuée pendant un parcours. Dans ce cas, elle passe à 1. Elle permet d’arrêter les parcours si sa valeur est restée à 0.

Tri par séparation

Le principe du tri par séparation consiste d’abord à séparer le tableau de valeurs en deux parties puis à trier chacune des parties indépendamment. Un algorithme de séparation consiste d’abord à choisir une valeur, appelée pivot. Puis à placer toutes les valeurs inférieures ou égales à gauche du pivot et les valeurs supérieures à droite du pivot. Il suffit alors de trier la partie gauche puis la partie droite du pivot sur le même principe. Pour réaliser ce tri, on fait appel à une technique particulière appelée la « récursivité ».

Pour illustrer le principe de séparation, considérons le tableau d’entiers ci-contre. On choisit la première valeur (50) comme pivot.

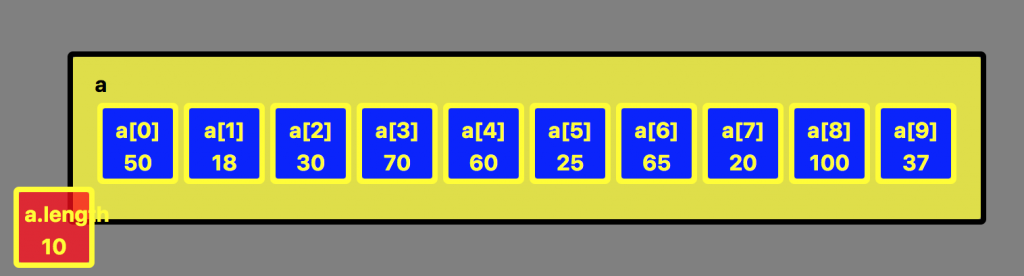
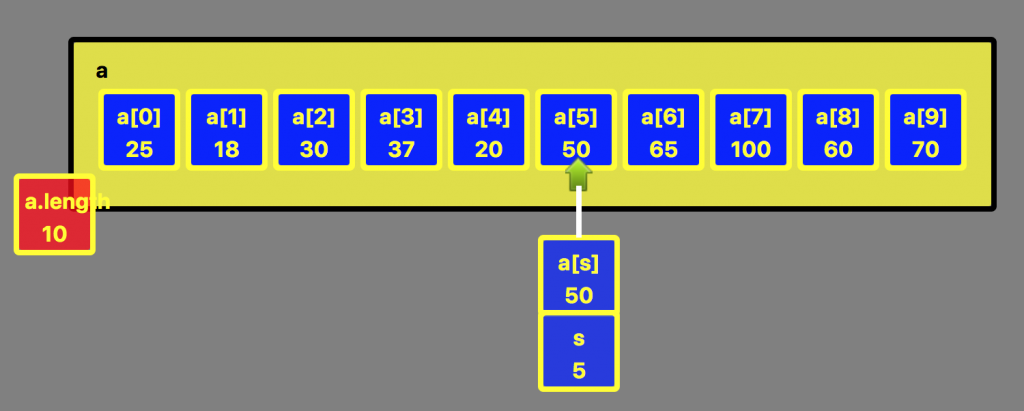
Après séparation, le pivot a été déplacé à l’indice 5. Toutes les valeurs d’indice inférieur sont inférieures au pivot et toutes les valeurs d’indice supérieur sont supérieures au pivot. 

Le tri par séparation est le tri le plus rapide, on l’appelle communément QuickSort. Ce tri ne peut être réalisé directement avec AlgoTouch puisqu’il nécessite la prise en charge de la récursivité. C’est une notion extrêmement puissante mais non abordée dans le cadre que nous avons choisi : l’apprentissage de la programmation à des débutants. Cependant, nous pouvons programmer un algorithme de séparation des valeurs d’un tableau. 

Un exemple de programme de séparation

Il existe de multiples façons de séparer un tableau. Voici par exemple un programme qui sépare un tableau a entre l’indice  g et l’indice d.

Le principe est le suivant :

  • on définit la valeur de a[g] comme pivot;
  • on parcourt le tableau d’entiers de gauche à droite;
  • tant que les valeurs sont inférieures ou égales au pivot, on avance;
  • lorsqu’on trouve une valeur plus grande, on la place vers la fin de tableau. Pour cela, on l’échange avec t[d], et on décrémente d. Ainsi les valeurs supérieures au pivot seront placées à la suite depuis la fin du tableau jusqu’à d (exclu);
  • le processus s’arrête lorsque la dernière valeur a été traitée.

Le résultat est un tableau dont toutes les valeurs « à gauche » sont inférieures ou égales au pivot et toutes les valeurs « à droite » sont supérieures au pivot. La variable s contient l’indice où a été déplacé le pivot. C’est donc l’indice qui désigne où s’est effectuée la séparation.

Avant de lancer le programme Partition, il faut vérifier que les indices g et d définissent bien les bornes du tableau de données à séparer.